In computer science, best, worst and average cases of a given algorithm express what the resource usage is at least, at most and on average, respectively. Usually the resource being considered is running time, but it could also be memory or other resources.
In real-time computing, the worst-case execution time is often of particular concern since it is important to know how much time might be needed in the worst case to guarantee that the algorithm will always finish on time.
Average performance and worst-case performance are the most used in algorithm analysis. Less widely found is best-case performance, but it does have uses: for example, where the best cases of individual tasks are known, they can be used to improve the accuracy of an overall worst-case analysis. Computer scientists use probabilistic analysis techniques, especially expected value, to determine expected running times.
The terms are used in other contexts; for example the worst- and best-case outcome of a planned-for epidemic, worst-case temperature to which an electronic circuit element is exposed, etc. Where components of specified tolerance are used, devices must be designed to work properly with the worst-case combination of tolerances and external conditions.
Best Case Performance
The term best-case performance is used in computer science to describe the way an algorithm behaves under optimal conditions. For example, the best case for a simple linear search on a list occurs when the desired element is the first element of the list.
In real-time computing, the worst-case execution time is often of particular concern since it is important to know how much time might be needed in the worst case to guarantee that the algorithm will always finish on time.
Average performance and worst-case performance are the most used in algorithm analysis. Less widely found is best-case performance, but it does have uses: for example, where the best cases of individual tasks are known, they can be used to improve the accuracy of an overall worst-case analysis. Computer scientists use probabilistic analysis techniques, especially expected value, to determine expected running times.
The terms are used in other contexts; for example the worst- and best-case outcome of a planned-for epidemic, worst-case temperature to which an electronic circuit element is exposed, etc. Where components of specified tolerance are used, devices must be designed to work properly with the worst-case combination of tolerances and external conditions.
Best Case Performance
The term best-case performance is used in computer science to describe the way an algorithm behaves under optimal conditions. For example, the best case for a simple linear search on a list occurs when the desired element is the first element of the list.
Examples
- Linear search on a list of n elements. In the worst case, the search must visit every element once. This happens when the value being searched for is either the last element in the list, or is not in the list. However, on average, assuming the value searched for is in the list and each list element is equally likely to be the value searched for, the search visits only n/2 elements.
- Insertion sort applied to a list of n elements, assumed to be all different and initially in random order. On average, half the elements in a list A1 ... Aj are less than element Aj+1, and half are greater. Therefore the algorithm compares the j+1-st element to be inserted on the average with half the already sorted sub-list, so tj = j/2. Working out the resulting average-case running time yields a quadratic function of the input size, just like the worst-case running time.
- Quicksort applied to a list of n elements, again assumed to be all different and initially in random order. This popular sorting algorithm has an average-case performance of O(n log n), which contributes to making it a very fast algorithm in practice. But given a worst-case input, its performance degrades to O(n2).






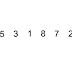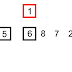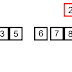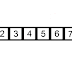
0 comments
Post a Comment