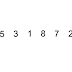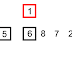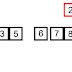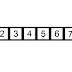Binary Search

In computer science, a binary search or half-interval search algorithm finds the position of a specified value (the input "key") within a sorted array. At each stage, the algorithm compares the input key value with the key value of the middle element of the array. If the keys match, then a matching element has been found so its index, or position, is returned. Otherwise, if the sought key is less than the middle element's key, then the algorithm repeats its action on the sub-array to the left of the middle element or, if the input key is greater, on the sub-array to the right. If the remaining array to be searched is reduced to zero, then the key cannot be found in the array and a special "Not found" indication is returned.

          A binary search halves the number of items to check with each iteration, so locating the an item (or determining its absence) takes logarithmic time. A binary search is a dichotomic divide and conquer search algorithm.

           Searching a sorted collection is a common task. A dictionary is a sorted list of word definitions. Given a word, one can find its definition. A telephone book is a sorted list of people's names, addresses, and telephone numbers. Knowing someone's name allows one to quickly find their telephone number and address.

If the list to be searched contains more than a few items (a dozen, say) a binary search will require far fewer comparisons than a linear search, but it imposes the requirement that the list be sorted. Similarly, a hash search can be faster than a binary search but imposes still greater requirements. If the contents of the array are modified between searches, maintaining these requirements may take more time than the searches! And if it is known that some items will be searched for much more often than others, and it can be arranged that these items are at the start of the list, then a linear search may be the best.

Program for Binary Search 

#include<stdio.h>
#include<iostream.h>
#include<iomanip.h>
#include<conio.h>
int bsearch(int a[],int low,int high,int ele);
void main()
{
int a[10],i,n,ele,found=0;
clrscr();
cout<<"enter the no of elements in to array";
cin>>n;
cout<<"enter elements in sorted order";
for (i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"enter the element to be searched";
cin>>ele;
cout.setf(ios::fixed|ios::left);
cout<<setw(10)<<"LOW"<<setw(10)<<"MID"<<setw(10)<<"HIGH";
cout<<endl;
found=bsearch(a,0,n-1,ele);
if(found==-1)
cout<<"element not found";
else
cout<<"element found at location "<<found;
getch();
}
int bsearch(int a[],int low, int high, int ele)
{
if(low<=high)
{
int mid =(low+high)/2;
cout<<setw(10)<<low;
cout<<setw(10)<<mid;
cout<<setw(10)<<high;
cout<<endl;
if(ele==a[mid])
return mid;
else if(ele<a[mid])
high=mid-1;
else if(ele>a[mid])
low=mid+1;
bsearch(a,low,high,ele);
}
else
return -1;
}

Read Full

Linear Search

In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found.
           Linear search is the simplest search algorithm; it is a special case of brute-force search. Its worst case cost is proportional to the number of elements in the list; and so is its expected cost, if all list elements are equally likely to be searched for. Therefore, if the list has more than a few elements, other methods (such as binary search or hashing) will be faster, but they also impose additional requirements.
For a list with n items, the best case is when the value is equal to the first element of the list, in which case only one comparison is needed. The worst case is when the value is not in the list (or occurs only once at the end of the list), in which case n comparisons are needed.
If the value being sought occurs k times in the list, and all orderings of the list are equally likely, the expected number of comparisons is

For example, if the value being sought occurs once in the list, and all orderings of the list are equally likely, the expected number of comparisons is . However, if it is known that it occurs once, then at most n - 1 comparisons are needed, and the expected number of comparisons is

(for example, for n = 2 this is 1, corresponding to a single if-then-else construct).
Either way, asymptotically the worst-case cost and the expected cost of linear search are both O(n).

Non-uniform probabilities

The performance of linear search improves if the desired value is more likely to be near the beginning of the list than to its end. Therefore, if some values are much more likely to be searched than others, it is desirable to place them at the beginning of the list.
In particular, when the list items are arranged in order of decreasing probability, and these probabilities are geometrically distributed, the cost of linear search is only O(1). If the table size n is large enough, linear search will be faster than binary search, whose cost is O(log n).

Program for linear search 

#include<stdio.h>
#include<iostream.h>
#include<iomanip.h>
#include<conio.h>
int lsearch(int a[],int,int);
void main()
{
int a[10],i,n,ele,found=0;
clrscr();
cout<<"enter the no of elements in to array";
cin>>n;
cout<<"enter elements ";
for (i=0;i<n;i++)
{
cin>>a[i];
}
cout<<"enter the element to be searched";
cin>>ele;
found=lsearch(a,ele,n);
if(found==-1)
cout<<"element not found";
else
cout<<"element found at location "<<found;
getch();
}
int lsearch(int a[],int ele,int n)
{
int i,c=0;
for(i=0;i<n;i++)
{
if(a[i]==ele)
{
return i;
c++;
}
}
if(c==0)
return -1;
}

Read Full

Fibonacci Series printing using Functions

#include<iostream.h>
#include<conio.h>
#include<iomanip.h>
void fibonacci(int );
void main()
{
int n;
clrscr();
cout<<"Enter a digit to findout fibonacci around it's range";
cin>>n;
fibonacci(n);
getch();
}
void fibonacci(int x)
{
int a=0,b=1,c;
cout<<a<<"\t"<<b;
while(c<x)
{
c=a+b;
a=b;
b=c;
cout<<"\t"<<c;
}
}
 

Read Full

Factorial Using Recursion

Proram for Factorial using recursion 

#include<iostream.h>
#include<conio.h>
#include<iomanip.h>
long int factorial(int );
void main()
{
long int f;
int n;
cout<<"Enter a digit to findout it's factorial";
cin>>n;
f=factorial(n);
cout<<"Factorial is"<<f;
getch();
}
long int factorial(int x)
{
while(x>=0)
{
if(x==0)
return 1;
else
{
int n=x*factorial(x-1);
return n;
}
}
}

Read Full

Pass by Value(swapping)

Program for Passby Value-PARAMETER PASSING 

#include<iostream.h>
#include<conio.h>
void swap(int,int);
void main()
{
int a,b;
cout<<"Enter any two numbers";
cin>>a>>b;
swap(a,b);
cout<<"\n the swapped valuesin the main funtion are"<<a<<"and"<<b;
getche();
}
void swap(int x,int y)
{
int t;
t=x;
x=y;
y=t;
cout<<"\n the  swapped values in the function are"<<x<<"and"<<y;

}

Read Full